Skip to content

Regresión lineal con Tensorflow 2+ | Simplemente fácil

En este artículo, nos ensuciamos las manos con una regresión lineal muy básica usando la versión reciente de tensorflow.

La regresión lineal generalmente se considera como el primer primer paso en el mundo de los algoritmos.

 ¿Qué es la regresión lineal?

  • La regresión lineal en términos fáciles es una línea recta que pasa cerca de todos los puntos de datos que trazamos.

    Técnicamente, la regresión lineal nos proporciona la relación entre una o más variables. La regresión lineal es un primer paso para todos los entusiastas de ML y se utiliza para el análisis predictivo y el modelado.

    Nuestro maestro dijo una vez cada vez, y = mx + b es una ecuación lineal y es verdad incluso hoy.

    A continuación se muestra un gráfico de regresión lineal entre años de exp. vs salario. Digamos que queremos predecir X = 1.2. Simplemente podemos extender la línea de lectura y obtener el valor en ese momento.

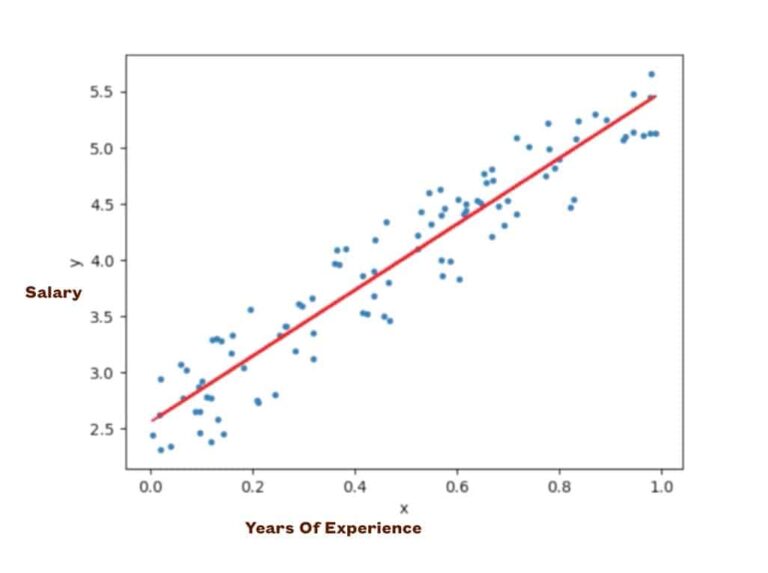
Linear Regression

Algunos hechos sobre la regresión lineal

  • Los principales tipos de regresiones incluyen Regresión lineal, Regresión polinómica, Regresión de cresta, Regresión de lazo.
    Excepto la regresión lineal, el resto de los tipos son adecuados para el análisis de datos de dimensiones superiores.

    La regresión lineal es una excelente manera de comenzar el viaje del aprendizaje automático, ya que es bastante sencillo y su primer paso para usar modelos en el mundo del aprendizaje automático.

¿Cómo podemos implementar la regresión lineal desde cero?

  • Suponga que x es la característica ey es el objetivo (y = mx + c). 
    Para encontrar el valor de myc, primero debe calcular la media de x e y,

    Algoritmo a continuación:


    Paso 0: calcule la media de x e y

    Paso 1: número total de registros
    n = len (x)


    Paso 2: siga estos pasos para calcular m y c.
    (Básicamente estamos capturando la distancia de un punto desde su media)

    numerador = 0
    denominador = 0
    para i en rango (n):
    numerador + = (X [i] – mean_x) * (Y [i] – mean_y)

    denominador + = (X [i] – mean_x) ** 2

    Paso 3: m = numerador / denominador

    Paso 4: c = media de y – (m * media de x)

    Entonces ahora tenemos m y c. ¡Qué podemos usar para hacer más predicciones!

¿Dónde podemos usar la regresión lineal?

  • Estimación del precio de una casa después de 2 años.

    Valor predictivo de una participación de 5 años.

    Predicción de la cantidad de lluvia para los próximos días.

    Y muchos más lugares donde queremos pronosticar un valor continuo.

Aquí estamos implementando un regresor lineal usando tensorflow con datos creados manualmente.

Antes de comenzar, ¡algunos requisitos previos!

 
Versión de Pythonnivel de dificultadRequisito previo
2.7+fácilfundamentos de python
Descargue el archivo de entrada de THIS LINK. 
”’
Importar módulos
”’
import tensorflow as tf
import numpy as np
import pandas as pd

import matplotlib.pyplot as plt

%matplotlib inline
 
 
”’
Leer los datos en famas de datos
El archivo tiene 2 columnas. 1: año y 2: valor
”’
df = pd.read_csv(‘sample_file.csv’, header=None)
# Make X a 2-D array of size N x D where D = 1 / .values converts series to numpy arrray
X = df.values[:,0] #.reshape(-1, 1)

Y = df.values[:,1]

”’
Graficar los datos: es exponencial
”’
plt.scatter(X, Y)
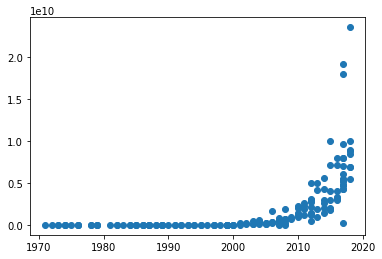
tensorflow_1
# Como queremos un modelo lineal, tomamos el registro
Y = np.log(Y)
plt.scatter(X, Y)
tensorflow_2
”’
Recuerde escalar los datos
”’
X = X – X.mean()
 
”’
Creemos una estructura de modelo TensorFlow aquí
”’
model = tf.keras.models.Sequential([
tf.keras.layers.Input(shape=(1,)),
tf.keras.layers.Dense(1)
])
”’
Compila el modelo
”’
model.compile(optimizer=tf.keras.optimizers.SGD(0.001, 0.9), loss=‘mse’)
”’
Establecer tasa de aprendizaje
”’
def lean_rate(epoch, lr):
if epoch >= 50:
return 0.0001
else :
return 0.001
scheduler = tf.keras.callbacks.LearningRateScheduler(lean_rate)

”’
entrenar al modelo
”’
fit = model.fit(X, Y, epochs=200, callbacks=[scheduler])
 
 
Epoch 199/200 6/6 [==============================] - 0s 2ms/step - loss: 0.9062 - lr: 1.0000e-04 
Epoch 200/200 6/6 [==============================] - 0s 2ms/step - loss: 0.8759 - lr: 1.0000e-04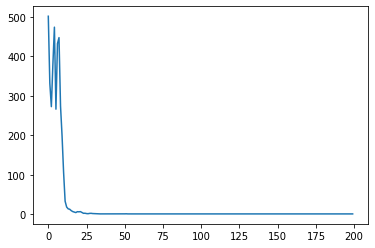
”’
Tracemos los resultados
”’
# Plot the loss
plt.plot(fit.history[‘loss’], label=‘loss’)
tensorflow_3
”’
Nuestra red tiene una sola capa.
Permite mostrar el valor de m & b en la ecuación lineal y = mx + b
”’
print(model.layers)
print(model.layers[0].get_weights())
[] [array([[0.33869487]], dtype=float32), array([17.776506], dtype=float32)]

Bien, ¡hagamos predicciones!

”’
Usamos la misma X para predecir
”’
pred = model.predict(X).flatten()
plt.scatter(X, Y)
plt.plot(X, pred)
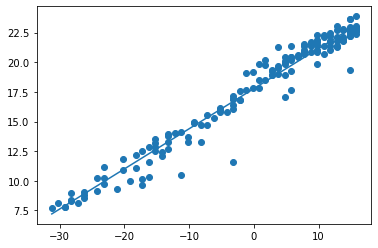
tensorflow_5
”’
Verifiquemos si nuestro modelo es exacto
”’
#Obtenemos el peso (w) y el sesgo (b)
w, b = model.layers[0].get_weights()

 

#Nosotras aplicamos y = mx + b
pred2 = (X.dot(w) + b).flatten()

 

# Verificamos si la salida de pred (calculada por modelo) y pred2 (pediculada manualmente)
#están cercanas entre sí
np.allclose(pred, pred2)
True

Wow, creamos una regresión lineal básica usando la versión más reciente de TensorFlow.

 ¡Te pueden gustar estos heroicos recientes a continuación!

Tags: