Skip to content

Recursion In Python With Examples | Memoization

RecursionFM

Tired of loops executing same logic again and again but with different values ? Recursion is here for your rescue !
Today we gonna cover recursion in Python with detailed examples and couple of real world problems.

What To Expect From This Blog ?

  • Recursion with types and real world examples.
  • Memoization and its significance.

Distraction alert : You may love to understand how are arrays developed in python from scratch. Refer here for an amazing article.


1. What Is Recursion?

The art of calling same current function again and again to get our final results can be termed as recursion.
Confused ? Keep reading. Examples below would make things clear.

2. Different Types Of Recursion

  • There are two main instances of recursion. The first is when recursion is used as a technique in which a function makes one or more calls to itself.
  • The second is when a data structure uses smaller instances of the exact same type of data structure when it represents itself.

    Both of these instances are use cases of recursion.


3. Why use Recursion?

Recursion provides a powerful alternative for performing repetitions of tasks in which usage of loop is not ideal.

Almost all modern programming languages support recursion and recursion is a great tool for building out particular data structures or solving real world problems.

4. Factorial Example

Lets dive IN !
We shall now see recursion through an example exercise of creating the factorial function.

The factorial function is denoted with an exclamation point and is defined as the product of the integers from 1 to n. Formally, we can state this as:n!=n·(n−1)·(n−2)…3·2·1

Note, if n = 0, then n! = 1. This is important to take into account, because it will serve as our base case.

Take this example:4!=4·3·2·1=24.So how can we state this in a recursive manner? This is where the concept of base case comes in.

Base case is a key part of understanding recursion, especially when it comes to having to solve interview problems dealing with recursion. Let’s rewrite the above equation of 4! so it looks like this:4!=4·(3·2·1)=24

Notice that this is the same as:4!=4·3!=24
Meaning we can rewrite the formal recursion definition in terms of recursion like so:n!=n·(n−1)!

Note, if n = 0, then n! = 1. This means the base case occurs once n=0, the recursive cases are defined in the equation above.

Whenever you are trying to develop a recursive solution it is very important to think about the base case, as your solution will need to return the base case once all the recursive cases have been worked through.

Let’s look at how we can create the factorial function in Python:

def factorial(n):
    '''
    Returns factorial of n (n!).
    '''
    # BASE CASE!
    if n == 0:
        return 1
    
    # Recursion!  Checkout function : factorial called again
    else:
        return n * factorial(n-1)

factorial(5)
Out[1]: 120

4.1 Lets Visualise the flow


We see in the program , the function factorial is called again and again until the base case is achieved !
Still unclear ?

Let’s visualise the results after every iteration.

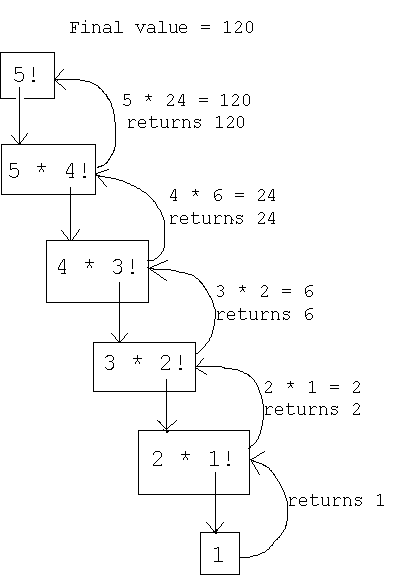
Recursion
Credits : http://faculty.cs.niu.edu/~freedman/241/241notes/recur.gif


Checkout the flow , that visualises the return type after every recursion call. We can follow this flow chart from the top, reaching the base case, and then working our way back up.

That should clear up things and give us an idea behind recursion !

5. Few Real Classic Examples Of Recursion

5.1 : Write a recursive function which takes an integer and computes the cumulative sum of 0 to that integer

For example, if n=5 , return 5+4+3+2+1+0, which is 15.

def recursive_sum(n):
    
    #base case 
    if n == 0 :
        return n 
    
    #main recursion logic
    return n + recursive_sum(n-1)
    

recursive_sum(5)
15


5.2 : Given an integer, create a function which returns the sum of all the individual digits in that integer.

 For example: if n = 54321, return 5+4+3+2+1

def sumthenumber(n) :
    
    #base case 
    if n==0 : 
        return n
    
    #main recursion logic -- usage of modulo in recursion 
    return n%10 + sumthenumber(n//10)

sumthenumber(54321)
15


5.3 : Given an string,  reverse it using recursion

def rev_string(s):
    
    # Base Case
    if len(s) <= 1:
        return s

    # Recursion 
    return rev_string(s[1:]) + s[0]

rev_string("3211234")
4321123

Note : If you don’t catch the logic , try a print statement before return and checkout the output.

6. Memoization

Wikipedia has a great explanation on this topic but in simple terms , memoization means result caching.

It so happens many times that we do a recursive operation where we already know the results of previous iteration , yet we re-calculate the result again !

In these cases we cache /store the results and use it instead of re-calculations.

Don’t get me ? Checkout the program below. 

'''
A simple example for computing factorials using memoization in Python would be something like this 
'''

# Create cache for known results
factorial_memo = {}

def factorial(k):
    
    if k < 2: 
        return 1
    
    if not k in factorial_memo:
        factorial_memo[k] = k * factorial(k-1)
        
    return factorial_memo[k]



factorial(4)
Out[2]: 24

factorial_memo works out as a caching dict which we can use to lookup result of previous iteration.

Benefits include , there will be good amount of time saved plus re-calculations avoided , hence making program run faster.

For detailed info , wikipedia provides great source.

7. Final Say

Memoization and recursion indeed go hand in hand as recursion involves re-iterations and memoization provides intermittent caching.

Not always these two may cross ways but we need to be vigilant and use these techniques smartly and get better results.

Thanks for reading !

You may not want to miss these exciting posts :

Tags: