Skip to content

Hashing In Python From Scratch ( Code Included )

hashingImage


So we are running late to office ! This prime time, it’s always great to know where are our daily needy items placed , so that we can directly get them with big O O ( 1 ) instead of O ( n ). Hashing is a great technique to achieve this in programming world.

Lets cover hashing in python from scratch and also implement it in python without any builtin libraries.

Distraction alert :
You may love to understand how are arrays developed in python from scratch. Refer here.
or
How do recursion really work in programming wold and its drawbacks and replacements here.

What To Expect From This Blog ?

  • Hashing – What is it and few facts !
  • Hash Tables.
  • Hash Functions – Different types available.
  • Collision Resolution.
  • Implementing a Hash Table in Python from scratch.


1.Hashing

A data structure that can be searched in O(1) time. This concept is referred to as hashing

Lets Imagine our day to day activities.
Early morning when we wake up , we know where is our tooth paste & brush. We directly walk up and pick them up without having to search in different locations.

This very concept of finding an element with one shot or O ( 1 ) is called hashing. Sometimes when we cannot manage O ( 1 ) , we manage some place close by !

How ? Do read on !

2. Hash Tables

  • Hash table is a collection of elements which are stored in such a way as to make it easy to find them when we need.
  • Initially, the hash table contains no element so every slot is empty.
  • Each position of the hash table, slots, can hold an element and is named by an integer( index ) value starting at 0. For example, we will have a slot named 0, a slot named 1, a slot named 2, and so on.

We can implement a hash table by using a list with each element initialised to the Python value None.
Here is an empty hash table with size m=11.

emptyList
empty hash table


The mapping between an element and the slot where that element belongs in the hash table is called the hash function.

The hash function will take any element in the collection and return an integer in the range of slot names, between 0 and m-1.

So how should we use hash functions to map items to slots?

3. Hash Function

We can remember hash function as the king maker. Its the hash function which returns the index where we need to push our element to.

There are many hash functions existent , lets understand few of them.

3.1 Remainder Method

One of hash function we can use is the remainder method.

When presented with an element, the hash function is the element divided by the table size, this is then its slot number ( Index ) .

Let’s see an example!

  • Assume that we have the set of integer items 54, 26, 93, 17, 77, and 31. 
  • We’ve preassigned an empty hash table of m=11.
  • Our remainder hash function then is: h(item)=item%11

Let’s see the results as a table.

hashtable2
hash table index


We’re now ready to occupy 6 out of the  11 slots.

This is referred to as the load factor, and is commonly denoted by :
 λ = numberofitems / tablesize. Here its λ=6/11

hashtable3
hash table post load


Our hash table has now been loaded.


Accessing The Element :

  • When we want to search for an element, we simply use the hash function to compute the slot name for the element and then check the hash table to see if it is present.
  • This searching operation is O( 1 ), since a constant amount of time is required to compute the hash value and then index the hash table at that location.

Limitations :

You should be thinking, what if you have two elements that would result in the same location ( index ) ?

For example 44%11 and 77%11 are the same. This is known as a collision (also known as clash).
Read on for ways to handle collisions.

A hash function that maps each item into a unique slot is referred to as a perfect hash function.

Our ultimate aim is to create a hash function that minimises the number of collisions, is easy to compute, and evenly distributes the items in the hash table. 

Before that lets cover other type of hash functions.


3.2 Folding Method

The folding method for constructing hash functions begins by dividing the item into equal-size pieces (the last piece may not be of equal size). 

These pieces are then added together to give the resulting hash value.

  • If our element was the phone number 436-555-4601.
  • We would take the digits and divide them into groups of 2 (43 , 65 , 55 , 46 , 01 ).
  • After the addition, 43+65+55+46+01, we get 210.
  • If we assume our hash table has 11 slots, then we need to perform the extra step of dividing by 11 and keeping the remainder. i.e 210 % 11 is 1, so the phone number 436-555-4601 hashes to slot 1.

Limitations :

Limitations are same as limitations in reminder method.

3.3 Mid Square Method

In the mid-square method we first square the element, and then extract some portion of the resulting digits. For example, if the item were 44, we would first compute 442=1,936.

By extracting the middle two digits, 93, and performing the remainder step, we get 93%11 =5.

Limitations :

Limitations are same as limitations in reminder method.

3.A Comparing Results

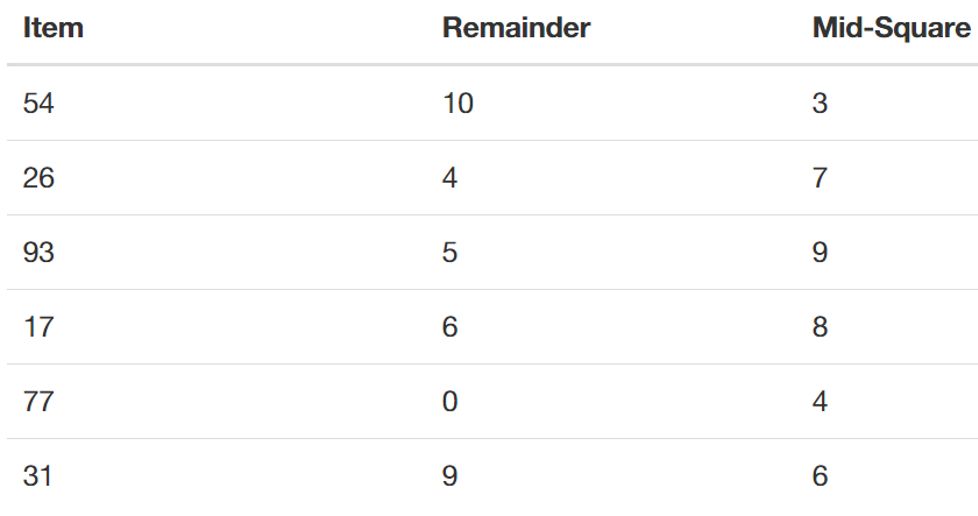
hashFunctionsResults
hashFunctionsResults

Columns 2 and 3 are the indexes generated for a hash table by using 2 different methods i.e remainder & mid-square.

3B. Handling Non-integer elements

We create hash functions for character-based items such as strings. The word “cat” can be thought of as a sequence of ordinal values.

ordinals
ordinals for “cat”

We use these ordinal values and then follow the same hashing techniques as discussed above.

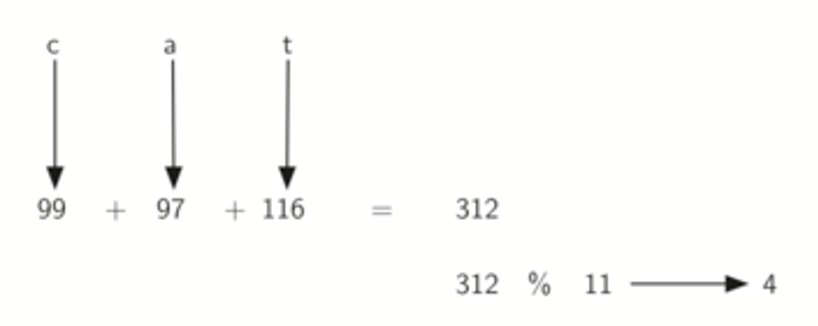
hash_cat
hash_cat

312 % 11 returns 4 and hence thats our hash index.

4. Collision Resolution

We have seen all the above hash function methods have same limitation. A mod function may return same index for multiple values. Thats called collision or clash.

Lets see few methods to avoid collusions.

4.1 Find nearby open slots

  • One method for resolving collisions looks into the hash table and tries to find another open slot to hold the element that caused the collision.
  • We can start at the original hash value position and then move in a sequential manner through the slots until we encounter the first slot that is empty.
  • This collision resolution process is referred to as open addressing in that it tries to find the next open slot or address in the hash table.
  • Systematically visiting each slot one at a time, we are performing an open addressing technique called linear probing.

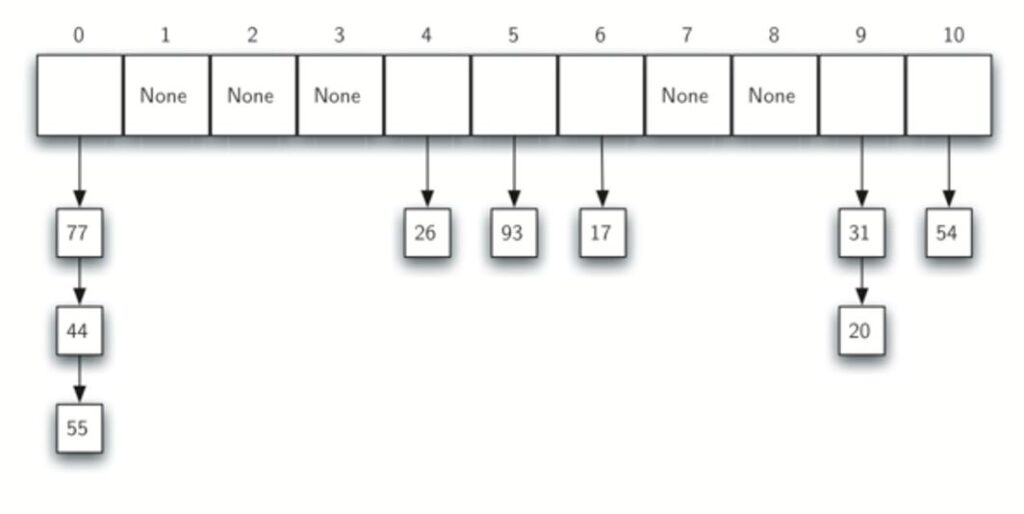
Consider the following table. What if we had to add 44 , 55, and 20 ?

collision-1
collision-1

With linear probing we keep moving down until we find an empty slot.

collision-2
collision-2

In general name for this process of looking for another slot after a collision is rehashing. 
One way to deal with clustering is to skip slots, thereby more evenly distributing the items that have caused collisions. 

skip-collided-elements
skip-collided-elements

4.2 Chaining

An alternative method for handling the collision problem is to allow each slot to hold a reference to a collection (or chain) of elements. Chaining allows many items to exist at the same location in the hash table.

When collisions happen, the item is still placed in the proper slot of the hash table. 

chaining
chaining



5. Implementing Hash Tables From Scratch ( Code )

'''
Note : We build this hash function for integer input only. If we need characters , we just need to add a function to calculate ordinality of each characters. 
'''

class HashTable(object):
    
    def __init__(self,size):
        
        # We set up size and slots and data
        self.size = size
        self.slots = [None] * self.size
        self.data = [None] * self.size
        
    def put(self,key,data):
        
        # We get the hash value
        hashvalue = self.hashfunction(key,len(self.slots))

        # in case Slot is Empty
        if self.slots[hashvalue] == None:
            self.slots[hashvalue] = key
            self.data[hashvalue] = data
        
        else:
            
            # If the key already exists, replace old value
            if self.slots[hashvalue] == key:
                self.data[hashvalue] = data  
            
            # Otherwise, find the next available slot - collision case
            else:
                
                nextslot = self.rehash(hashvalue,len(self.slots))
                
                # Get to the next slot
                while self.slots[nextslot] != None and self.slots[nextslot] != key:
                    nextslot = self.rehash(nextslot,len(self.slots))
                
                # Set new key, if NONE
                if self.slots[nextslot] == None:
                    self.slots[nextslot]=key
                    self.data[nextslot]=data
                    
                # Otherwise replace old value
                else:
                    self.data[nextslot] = data 

    def hashfunction(self,key,size):
        # Remainder Method
        return key%size

    def rehash(self,oldhash,size):
        # For finding next possible positions
        return (oldhash+1)%size
    
    
    def get(self,key):
        
        # Get the  items given a key
        
        # Set up variables for our search
        startslot = self.hashfunction(key,len(self.slots))
        data = None
        stop = False
        found = False
        position = startslot
        
        # Until we discern that its not empty or found (and haven't stopped yet)
        while self.slots[position] != None and not found and not stop:
            
            if self.slots[position] == key:
                found = True
                data = self.data[position]
                
            else:
                position=self.rehash(position,len(self.slots))
                if position == startslot:
                    
                    stop = True
        return data

    # Special Methods for use with Python indexing
    def __getitem__(self,key):
        return self.get(key)

    def __setitem__(self,key,data):
        self.put(key,data)
  • HashTable() Create new empty map. return : an empty map collection.
  • put(key,val) Add a new key-value pair to the map. If the key is already in the map then replace the old value with the new value.
  • get(key) For a key, return the value stored in the map or None otherwise.

Lets verify the output comes : 

h = HashTable(5)
In [5]:

# insert our first key : 
h[1] = 'twenty one'
h[2] = 'twenty two'

print(h[1]) 
'twenty one'

That seems like have worked 🙂 Similarly we can implement del function , IN function etc to match up with other python data structure operations like list , dict etc.

6. Final Say

That was amazing way to understand and implement hashing from scratch.
Note , in real world , Python already has dictionary ( {} ) whose underlying logic is same as we discussed.

Having the knowledge on how these amazing data structures were built , gives us a better hold and understanding a section of how the mighty python language as built.

Thanks for reading !

You may not want to miss these exciting posts :


Tags: