Comencemos con nuestra primera publicación sobre estructuras de datos y algoritmos y aquí hablaremos principalmente sobre arreglos . También crearemos esta estructura de datos desde cero sin utilizar bibliotecas integradas .
Las estructuras de datos y los algoritmos forman una parte importante de las entrevistas en las principales empresas. Conocerlos no solo lo ayudará a descifrar uno, sino también a comprender cómo funcionan los conceptos básicos de los programas de computadora.
¿Qué esperar de este blog?
- Matrices en detalle.
- Diferentes tipos de matrices.
- Cómo Python administra la memoria durante las operaciones de matriz.
- Crea nuestra propia matriz desde cero 🙂
1. Matrices en detalle
Justo antes de comenzar con las matrices en detalle , siempre es asombroso saber cómo nuestra computadora almacena la información en la memoria .
Recuerda :
- La medida más pequeña del tamaño de la información son los bits .
- En las computadoras, normalmente medimos el tamaño más pequeño de datos en bytes . Un byte es igual a 8 bits .
- Para cada información almacenada en la memoria como bytes, tienen una identificación única para ellos mismos. es decir, considere la palabra ‘A B’. A tendrá un ID XXXX seguido de B YYYY .
- Todo el almacenamiento y la recuperación de información se realiza a través de este ID único (índice). Nuestros hardware de computadora están diseñados de tal manera que respalden estas operaciones . Cuando escribimos un programa, digamos python o Scala, estos programas mantienen un registro de los almacenamientos e índices .
- Entonces , finalmente , toda esta información se escribe o se lee desde la MEMORIA DE ACCESO ALEATORIO o la RAM .
Entonces, finalmente comencemos con matrices en Python 😛
1.1 ¿Python tiene matrices?
Si tenemos algo de experiencia en Python, probablemente nunca escuchemos el nombre de ” matrices ” cuando codificamos. En cambio, escuchamos nombres como listas , tuplas . Estos no son más que matrices en Python. Entonces, de ahora en adelante, cuando nos referimos a matrices, en Python hace referencia directamente a listas o tuplas .
1.2 Arreglos de bajo nivel Vs Arreglos referenciales
Python suele tener 2 tipos de matrices. Las matrices de bajo nivel generalmente significan que los datos se almacenarán como bytes en bloques de memoria regulares , mientras que la referencia tiene el concepto de punteros. Discutiremos esto en detalle a continuación para aclarar los conceptos.
Comencemos con matrices de bajo nivel.
Aquí, Python representa internamente cada carácter como 2 bytes, es decir, 16 bits. Considere la palabra ” Muestra “.

Observe la palabra ” S “, tiene 2 índices 2146 y 2147 . Esto significa que una palabra se representa en 2 bytes . Un total de 6 caracteres se almacena como 12 bytes .
Ahora imagine que necesitamos almacenar 1000 empleados con sus ID de empleado . Aunque podemos usar el método anterior, es muy ineficiente .
Aquí, las matrices referenciales entran en escena. En matrices referenciales almacenamos datos como se muestra a continuación,
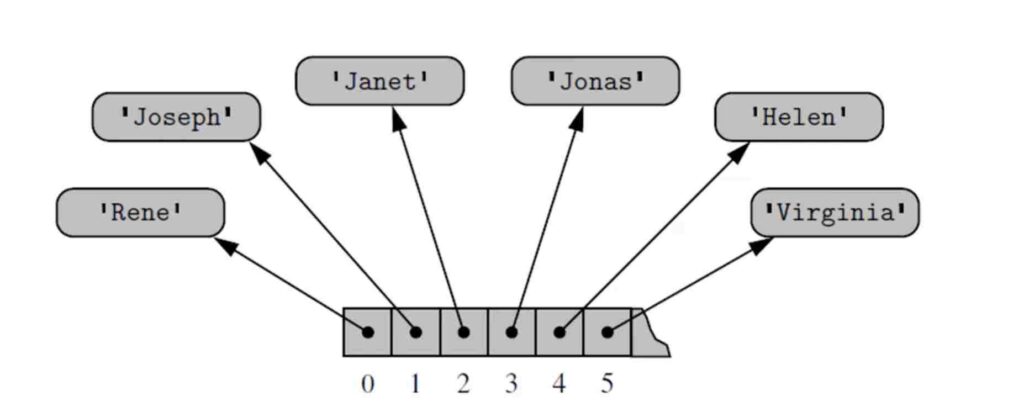
Se puede notar que cada índice se apuntó a un determinado objeto . Así es como funcionan las matrices referenciales .
Python es lo suficientemente inteligente como para apuntar duplicados al mismo índice, lo que ayuda a ahorrar memoria. Verifique a continuación.
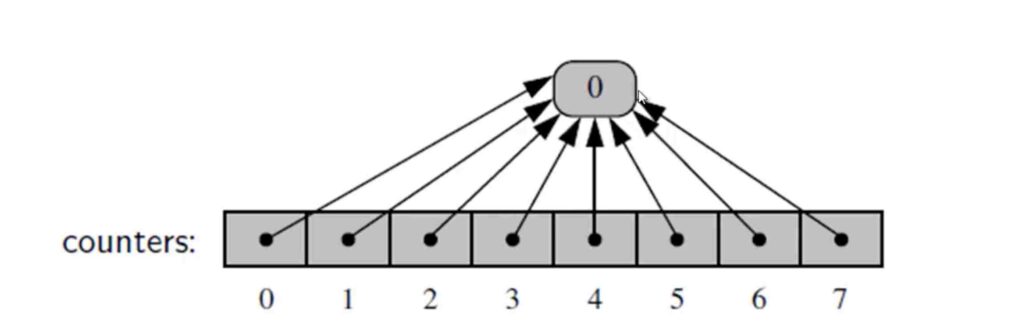
Cuando su matriz es de tamaño 8 y todos los valores son ceros , Python hará referencia a ella como se indica arriba para ahorrar una gran cantidad de memoria.
Entonces, ¿qué pasa si se actualiza una parte de la matriz ? ¡Python lo maneja de esta manera!
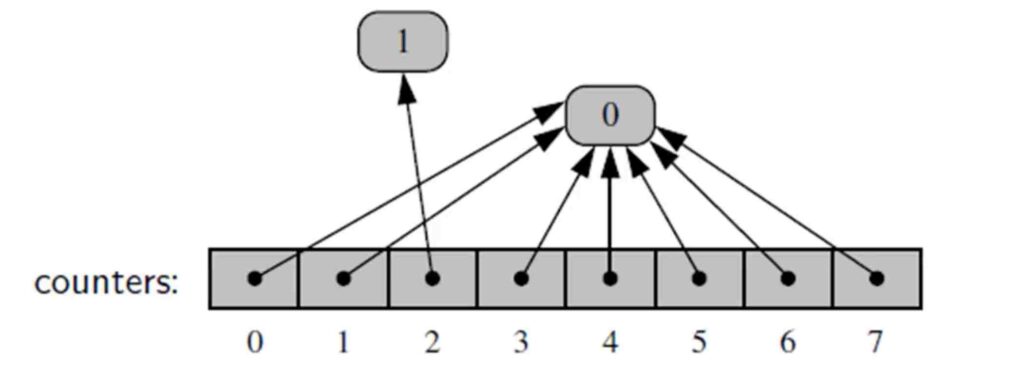
Se crea un nuevo objeto de referencia solo para un valor actualizado .
¿No es asombroso ? Ahora consideremos un último escenario de ampliación de listas . Los bloques de memoria se verán como se muestra a continuación.
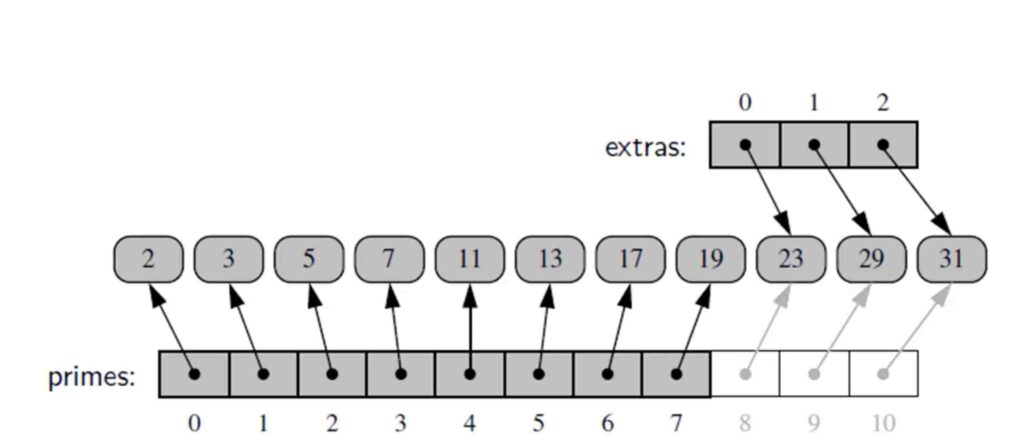
Python asigna una nueva lista de índices cuando se amplía una lista . es decir, tendría un enlace principal a la nueva losa de índice y un enlace secundario a la losa de índice existente, como se muestra arriba.
Esto ayuda enormemente cuando se realizan operaciones de actualización o modificación para que sucedan de manera eficiente . Este proceso continúa a medida que se amplía una matriz .
Si no pudiste captar esto, ¡espera! La siguiente sección puede ayudarlo a tener una idea.
1.3 ¿Qué son las matrices dinámicas? Un cambio de juego para Python perf.
Así que hemos analizado varias formas en que una matriz se almacena en la memoria. Ahora, en el mundo práctico real , a menudo usamos matrices para almacenar una gran cantidad de datos y Python tiene que extender constantemente su asignación de memoria .
Aunque todo sucede automáticamente , vamos a tener una idea de cómo Python lo hace todo por sí solo dejando menos carga en la recolección manual de basura .
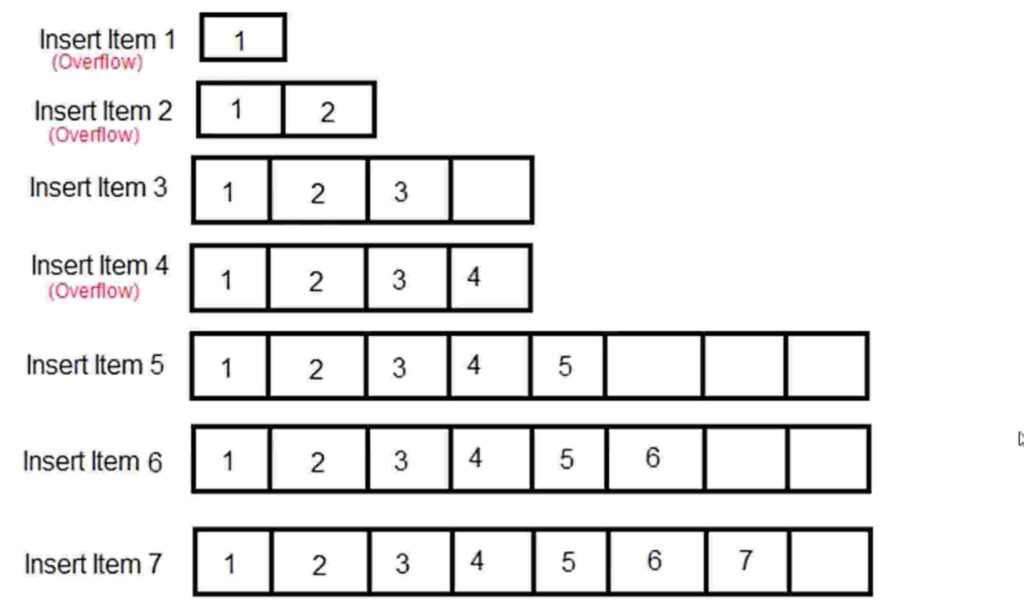
Bueno, veamos un escenario de insertar elementos 1-10 en una matriz vacía . La naturaleza dinámica de las matrices de Python funciona de la siguiente manera.
- Inserte 1 y la memoria predeterminada asignada a la lista sería de 2 bytes (1 bloque). Esto resulta en un desbordamiento.
- Ahora, el intérprete de Python crea una matriz FRESCA con el doble de memoria a 4 bytes (2 bloques). El contenido de 1 se copia en esta nueva matriz. La matriz antigua se somete a recolección de basura . Pero aún así, esta matriz se desborda.
- El intérprete de Python crea otra matriz FRESCA del doble del tamaño con 4 bloques y copia el contenido anterior en una nueva matriz nueva. Se descarta la matriz más antigua .
- El proceso continúa hasta que finaliza la ejecución .
Ahora sabemos cómo ocurre una gestión real de la memoria en Python . El concepto es muy simple.
Una vez que una lista o tupla de memoria se desborda , el intérprete crea una nueva lista o tupla de doble tamaño y copia todo a la recién creada nueva matriz. Se descarta la matriz más antigua .
2. Creación de matrices desde cero
Aquí intentamos crear nuestra propia estructura de datos (similar a la lista ) usando Python .
import ctypes
class OurOwnList(object):
def __init__(self):
# Contar elementos reales (el valor predeterminado es 0)
self.n = 0
# Default Capacity
self.capacity = 1
self.A = self.make_array(self.capacity)
def __len__(self):
"""
Devuelve el número de elementos ordenados en una matriz
"""
return self.n
def __getitem__(self,k):
"""
Devolver elemento en el índice k
"""
if not 0 <= k <self.n:
# Verifique que el índice k esté dentro de los límites de la matriz
return IndexError('K is out of bounds!')
#Recuperar de la matriz en el índice k
return self.A[k]
def append(self, ele):
"""
Agregar elemento al final de la matriz
"""
if self.n == self.capacity:
self._resize(2*self.capacity) #Doble capacidad una vez desbordado
self.A[self.n] = ele #Establecer índice self.n en elemento
self.n += 1
def _resize(self,new_cap):
"""
Cambiar el tamaño de la matriz interna a la capacidad newcap
"""
B = self.make_array(new_cap) # Nueva matriz más grande
for k in range(self.n): # Hacer referencia a todos los valores existentes
B[k] = self.A[k]
self.A = B # Llame a A the fresh array
self.capacity = new_cap # Restablecer la capacidad
def make_array(self,new_cap):
"""
Devuelve una nueva matriz con capacidad new_cap
"""
return (new_cap * ctypes.py_object)()
He incluido comentarios sobre la funcionalidad de todas las funciones anteriores. Está bien si no capta todo, pero este fue un intento de crear nuestras propias estructuras de datos desde cero .
Verifiquemos la salida de nuestra nueva estructura de datos OurOwnList 🙂
# Instancia de la clase
arr = OurOwnList()# Agregar nuevo elemento
arr.append(10)# Agregar otro elemento
arr.append(12)# Compruebe la longitud de la matriz
len(arr)
#salida : 2# acceder a los elementos a través del índice
arr[1]
#salida : 12¡Uf ! funcionó.
3. Acceso a elementos en una matriz: específico de Python
Tenemos que recordar que todas las matrices de Python comienzan desde el índice CERO (0).
Si vemos alguna secuencia de matriz con corchetes ” [] ”, son listas y una con “ () ” son tuplas .
Ej: a = [1,2,3]. es una lista. mientras que (1,2,3) es una tupla. (Observe los corchetes)
Para acceder a cualquier elemento , simplemente podemos usar a (0) para el primer elemento a (1) para el segundo y así sucesivamente.
Se puede acceder al último elemento mediante [-1].
Puede leer más sobre la división de matricesaquí .
4. Finalizando
Ese fue un viaje emocionante de cómo funciona la lógica subyacente de las matrices de Python. También cubrimos cómo el intérprete de Python administra la memoria y descarta elementos que ya no son necesarios.
Aunque python se encarga automáticamente de la mayoría de las recolecciones de basura , siempre es bueno saber cómo se desarrollan las estructuras de datos del lenguaje Python.
Gracias por leer !
Es posible que no desee perderse estas emocionantes publicaciones:
- Estructuras de datos en Python: pilas, colas y deques
 Series de estructuras de datos en python que cubren pilas en python, colas en python y deque en python con su implementación desde cero.
Series de estructuras de datos en python que cubren pilas en python, colas en python y deque en python con su implementación desde cero. - Estructuras de datos en Python – Arrays | Créalos desde cero
 Estructuras de datos en python. Este artículo cubre las matrices en Python y la implementación de matrices desde cero. Esto también cubre la gestión de la memoria de la matriz.
Estructuras de datos en python. Este artículo cubre las matrices en Python y la implementación de matrices desde cero. Esto también cubre la gestión de la memoria de la matriz. - Redes neuronales recurrentes en pocas palabras | Guía A-Z
 ¿Qué es una red neuronal recurrente? Un tipo especial de redes neuronales, también llamadas RNN, se usa ampliamente para tratar datos de secuencia.
¿Qué es una red neuronal recurrente? Un tipo especial de redes neuronales, también llamadas RNN, se usa ampliamente para tratar datos de secuencia. - Redes neuronales de convolución en pocas palabras | Guía de la A a la Z
 La red neuronal convolucional (ConvNet o CNN) es una red neuronal utilizada de manera efectiva para el reconocimiento y clasificación de imágenes. CNN no es menos que una caja mágica
La red neuronal convolucional (ConvNet o CNN) es una red neuronal utilizada de manera efectiva para el reconocimiento y clasificación de imágenes. CNN no es menos que una caja mágica - Clasificación lineal (regresión logística) utilizando reciente Tensorflow 2+En este artículo, implementamos la clasificación lineal utilizando la versión más reciente de Tensorflow. es decir, 2.2+ ¿Qué es la clasificación lineal ? Cuando los puntos de datos a clasificar son separables por una línea o, en términos más fáciles, podemos trazar una línea entre los registros de éxito y los registros de falla, lo llamamos Clasificador lineal . … Read More »Clasificación lineal (regresión logística) utilizando reciente Tensorflow 2+




